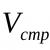Consumer budget line and its properties. Slope of the budget line
Each product in the set has a different price, the consumer's budget is limited, and then the consumer's choice becomes limited. The possible choice for the consumer is reflected by the budget line. Budget lines answer the question: what can a consumer buy with a certain monetary income, taking into account current prices for goods.
Budget line is the set of goods that a consumer is able to purchase at a given income and given prices.
The budget line indicates all combinations of goods for which the total cost is equal to income (Fig. 4.11.). If we plot on the x-axis the maximum number of units of one product that can be purchased with available funds, for example, food, and on the y-axis - the same for another product - clothing, then triangle OAB will contain all available options for the consumption of goods A and B, and on the segment AB - those of them that have the same total cost and involve the full use of the buyer’s financial resources. Points located to the right and above AB are inaccessible, because they correspond to an income greater than that available to the consumer. Points located to the left and below AB do not meet the condition that all income must be spent.
The budget line equation has a simple form:
I=Qx*Px+Qy*Py
where Qx and Qy are the quantities of goods of type x and y; Px and Py are their prices; I - total flow
Let us transform the equality as an equation of the quantity of one of the consumed goods:
We have obtained the equation of the budget line, or, as it is also called, the price line.
The budget line has a negative slope. If our amount of money (budget) has changed - it has become more or less, but the goods are the same, the corresponding budget straight lines will run parallel to the first straight line, with a smaller amount - closer to the origin of coordinates, with a larger amount - further from it, i.e. the distance from the origin determines the size of the budget.
All product bundles corresponding to points on the budget line are available to the consumer. Those. The budget line limits from above the set of product sets available to the consumer. Product sets located above and to the right of the budget line are not available to the consumer. Product sets located below the budget line are also available to the consumer, but their purchase does not allow the entire budget to be spent.
The location of the budget line depends on income and on the prices of goods. However, incomes and prices change frequently. How does the budget line change when income and prices of goods change? Suppose that the consumer's income is reduced to I"< I, цены на блага неизменны. Наклон бюджетной линии не изменится, так как он зависит лишь от пропорций цен. В этом случае произойдет параллельный сдвиг бюджетной линии вниз. Она займет положение K"L". При росте дохода и неизменных ценах наблюдается параллельный сдвиг бюджетной линии вверх. Допустим теперь, что доход и цена товара X неизменны, цена же блага Y уменьшилась до P"Y < PY. В данном варианте точка L не изменит своего положения, ибо оно обусловливается неизменными I и Рх. Левый же конец бюджетной линии сдвинется вверх и займет положение К".
If prices remain unchanged and income changes (increase or decrease), the buyer can increase or decrease purchases of goods. With stable income and changes in prices on the market, the situation develops depending on whether the price of one product or all included in the set changes. If the price of one product changes (rises or falls) and another remains unchanged, then the consumer can reduce or increase purchases of the product whose price has changed. The ratio of prices of goods P X (food) / P Y (clothing) determines the slope of the budget line. E If, with a fixed budget and a constant price of product X, the price of product Y decreases (increases), then the slope of the budget line decreases (increases), in other words, the budget line will rotate clockwise when the price increases and against it when the price decreases relative to any point of contact with the coordinate axes (Fig. 4.12.).

Rice. 4.12. The impact of price changes on the budget line.
So, the properties of the budget line:
1. Points A and B show the maximum possible volume of consumption of goods Y and X, respectively, i.e. the entire budget is spent only on product Y or product X, respectively.
2. Slope of the budget line = - Px / Py ; A minus sign indicates a negative slope.
3. When the consumer's income changes, the budget line moves in parallel. To the right - when income increases, to the left - when income decreases.

4. When prices for goods change, the angle of inclination of the budget line changes, and the consumer can buy more (less) of goods X (Y), i.e. The consumer's purchasing power may increase (as prices fall) or decrease (as prices rise). Income remains unchanged, prices increase (decrease) - rotation of the budget line to position AB 1 (AB 2); There remains only a single common point (point A), at which the buyer’s consumption possibilities have not changed.


If prices for both goods change proportionally, that is, increase or decrease by the same number of times (for example, with 10% inflation, all prices increase by 1.1 times), then the budget line will also move in parallel: if prices increase proportionally, the budget line will shift to the left and, conversely, a decrease in prices will move the budget line to the right.
5. If income and prices simultaneously increase proportionally (or simultaneously decrease proportionally), then the position of the budget line will not change. This is the meaning of indexing household incomes: an inflationary increase in prices, which leads to a parallel shift of the budget line to the left, is accompanied by a simultaneous proportional (i.e., the same number of times) increase in income (which shifts the budget line in parallel to the right), and the budget line, which means that the real welfare of consumers does not change.
Maximizing Demand.
Consumers make rational (optimal) choices in the market, i.e., they choose products in such a way as to achieve maximum satisfaction of their needs with a given limited budget. The optimal mix of consumer goods and services must meet two requirements. First, the choice from a set of bundles occurs within the limits of the consumer's income. Secondly, the optimal set of consumer goods and services should provide the consumer with their most preferred combination.
The simplest rule for maximizing utility is the rule of common sense: if you cannot increase utility by changing combinations of goods (consumption bundles), then you have achieved maximum utility and this consumption bundle is the best. Consequently, the set that provides maximum satisfaction of needs must be at the intersection of the indifference curve furthest from the origin with the budget line, because The indifference curve shows what the consumer would like to buy, and the budget line shows what the consumer can buy. Graphically this can be depicted like this:

Rice. 4.13. Schedule for maximizing customer satisfaction.
Consumer equilibrium is set at the point (given a given set of goods) when the highest possible level of utility is achieved under a given budget constraint. This is point E, which is called consumer optimum.
When a consumer maximizes satisfaction by consuming certain quantities of different goods (in our example, clothing and food), the marginal rate of substitution (or the ratio of the marginal utilities of two goods) is equal to the ratio of the prices of these goods purchased.
Knowing consumer choice under budget constraints, individual demand can be determined. The demand for a particular good depends on the prices of consumer goods and on the income allocated for consumption. The dependence of demand on the prices of consumer goods, and not on the price of the product for which demand is presented, is explained by the fact that the consumer constantly transforms the structure of demand, guided by changes in the prices of all components of the consumer set.
Example task:

The budget line equation is: I = y + 2x. Therefore, y = 30 – 2x.
| | | | 5 |
Budget area of the consumer
Consumer Indifference Map shows his subjective attitude towards a particular set of goods.
However, the consumer's ability to satisfy his tastes and preferences, and therefore the demand that he places on the market, depends on the income at his disposal and on the prices of the relevant goods.
Both of these factors together determine the area of consumer sets acceptable to the consumer, or the budget area.
Consumer budget constraint can be written as an inequality:
P 1 Q 1 + P 2 Q 2 ≤ R
- P 1 P 2 - prices for the corresponding goods Q 1 and Q 2
- R - consumer income
Budget line
If the consumer completely spends his income on goods Q1 Q2 then we get the equality:
P 1 Q 1 + P 2 Q 2 = R
Transforming this equality, we get budget line equation, having the form:

The budget line shows the set of combinations of goods Q1 and Q2 that a consumer can purchase by spending all of his money income. The slope of the budget line is determined by the ratio P1/P2.
In a multi-commodity economy and assuming consumer savings are taken into account, the budget line equation can be written in general form as follows:
P1Q1 + P2Q2 + ... +PnQn + savings = R
Budget line offset
A change in the budget area can occur under the influence of two main factors: changes in income and changes in prices for goods.
Increase in money income from R1 to R2 at constant prices will allow the consumer to purchase larger quantities of one or another product. The slope of the budget line will not change because prices remain the same, but the line itself will move up and to the right, parallel to itself. As income decreases, the line will move lower and to the left.

Change in the price of one of the goods with constant income and the price of another good will change the slope of the budget line, equal to the price ratio. So, for example, when the price P1 for good Q1 decreases, the maximum quantity of the good purchased with a given income increases from R/P11 to R/P12. Accordingly, the angle of inclination of the budget line decreases

- with a simultaneous n-fold increase in prices P1, P2, and income R, the position of the budget line does not change, and therefore, the area of budget constraints will remain the same.
- an increase in prices by n times is equivalent to a decrease in consumer income by the same amount.
Economic consumer behavior
Optimum point
An indifference map is a graphical representation of consumer tastes and preferences.
The budget area shows the totality of goods available to the consumer, that is, his purchasing power. Combining these graphs allows us to answer the question of which product mix is best for the consumer.
The bundle of goods that maximizes the consumer's total utility is called consumer equilibrium point (optimum point) and lies at the point of tangency between the budget line and the indifference curve (provided that the product is desirable for the consumer, that is, it has positive marginal utility).

Optimum conditions
For an optimal consumer set, the following conditions are met:- the equilibrium combination of goods (x*1,x*2) always lies on the budget line, and not below it. This means that in order to maximize utility, the consumer must fully use the available income (savings are also considered as a good that can be “purchased”);
- at the equilibrium point, the slope of the indifference curve is equal to the slope of the budget line, or
Angle of indifference curve = MRS = - Δx2/ Δx1,
Angle of inclination of the budget line = - P1/P2.
Hence, second condition for utility maximization assumes such a distribution of income by the consumer at which the marginal rate of substitution of one good for another is equal to the inverse ratio of their prices
MRS = - P1/P2,
Δх2/Δх1=Р1/Р2.
The economic meaning of this condition is MRS of good 2 by good 1 determines the level at which the consumer wants to replace one good with another. Price ratio ( P1/P2) determines the level at which the consumer can replace good 2 with good 1. Until these levels become equal, exchanges are possible that increase the total utility of the consumer.
The second maximization condition can be written differently. From the definition of marginal utility
MU1= ΔTU/ Δх1;
MU2= ΔTU / Δх2.
If we divide MU1 by MU2, we get
MU1/MU2 = Δx2/ Δx1,
MU1/MU2 = P1/P2.
This implies the equality
MU1/ P1 = MU2/ P2.
In the case of goods, the expression takes the form
MU1/P1= MU2/P2 = …= MUn/Pn = MU savings.
This means that the utility maximization conditions derived from indifference curve analysis (the ordinalist way) and the cardinalist utility model can be written in the same way.
The B. line is the locus of points characterizing all sets of two goods that a consumer can purchase after fully spending his income at given prices.
Budget restrictions, consumer, or personal, budget are the monetary income of the consumer, within which a demand can be made for goods and services that meet his needs.
Suppose that a consumer, having a fixed income, spends 100 rubles per day. to buy only two goods - A and B. If he spent all 100 rubles. to purchase product A, he would purchase it in the amount of 6 units. If these 100 rubles. were spent on the purchase of good B, then the consumer would have 8 units of this good. Within these values, he can spend 100 rubles. for the purchase of goods A and B in any combination. The MN line shows the consumer's limitations and is called the consumer opportunity line, or budget line.
The budget line (line of the budget constraint) is a straight line, the points of which show sets of goods, when purchasing which the consumer’s income is spent in full. Mathematically, the budget constraint can be expressed by the equation:
I = Ra * A + Pv * B
where I is consumer income; Ra is the price of good A; Рв - price of good B; A and B are goods needed by the consumer.
From the budget line equation it follows that the budget line has a negative slope. The angle of its inclination is determined by the price ratio, and the distance from the origin of coordinates is determined by the size of the budget.
If, at fixed prices of goods, the consumer's budget changes, then a parallel shift in the budget line occurs. The slope of the budget line will not change, since it is determined only by the price ratio. With an increase in income and constant prices, there will be a parallel upward shift in the budget line.
If, with a fixed budget and a constant price of good B, the price of good A changes, then the slope of the budget line changes. The budget line rotates around the point of intersection of the budget line with the vertical coordinate axis: the angle of inclination decreases when the price of the product becomes cheaper and increases when its price rises. This is explained by a change in the maximum quantity of consumption of good A. A consumer who behaves in such a way as to maximize utility with limited income is called a rational consumer; indifference curves have a negative slope. There is an inverse relationship between the quantities of goods X and Y. When the consumption of one good decreases, in order to compensate for losses and maintain the same level of utility, the consumer must increase the consumption of another good. Any curve expressing the feedback of variables has a negative slope;
Properties of the budget line:
- 1, indifference curves are convex with respect to the origin. It was noted above that when the consumption of one good increases, the consumer must reduce the consumption of another good. The convexity of the indifference curve relative to the origin is a consequence of the fall in the marginal rate of substitution.
- 2, the absolute value of the slope of the indifference curve is equal to the marginal rate of substitution. The slope of the indifference curve at a given point shows the rate at which one good can be replaced by another good without gain or loss of utility for the consumer. This ratio is characterized by the marginal rate of substitution;
- The 3 indifference curves do not intersect. The same consumer cannot characterize the same set of goods with different levels of utility. Therefore, two indifference curves representing different levels of utility cannot intersect;
- 4 it is possible to construct an indifference curve passing through any set of goods. An indifference curve can be constructed for any pair of goods that provide a certain level of utility. It is on this principle that an indifference map is constructed, which provides complete information about the consumer’s system of preferences.
Indifference curves allow us to identify consumer preferences, but do not take into account: prices of goods and consumer income. They do not determine which particular set of goods the consumer considers most profitable for himself.
This information is given to us by the budget constraint, which shows all combinations of goods that can be purchased by a consumer at a given income and given prices. Let I – consumer income, R X – price of the good, – consumer income, X X X, A – price of the good And X constitute, accordingly, the required quantities of goods. To simplify, we assume that the consumer does not make any savings and spends all his income on purchasing only two goods – price of the good And X.
The budget constraint equation will be: Let= P R · R+ P X · X. R And X The budget constraint has a fairly simple meaning: the consumer’s income is equal to the amount of his expenses for purchasing goods
. – Let us transform the budget constraint equation to the following form: .
Budget line (budget constraint line)
This is a straight line, the points of which show sets of goods, when purchasing which the consumer’s income is spent completely.
T
 The points of intersection of the budget line with the coordinate axes can be obtained as follows. If a consumer spends all his income only on purchasing a product
The points of intersection of the budget line with the coordinate axes can be obtained as follows. If a consumer spends all his income only on purchasing a product  –
, then he will be able to purchase X units of this product, similarly
–
, then he will be able to purchase X units of this product, similarly  units of goods R(Fig. 2.7). The slope of the budget line is X.
units of goods R(Fig. 2.7). The slope of the budget line is X.
coefficient of X in the budget line equation. The economic meaning of this slope is to measure the opportunity cost of goods, in this case the cost of one unit of goods R in units of goods X For example, product
– table wine priced at 20 thousand rubles. per bottle, and
– a soft drink priced at 5 thousand rubles. per bottle. Then, having bought one bottle less wine, the consumer has an additional 20 thousand rubles. to purchase four additional bottles of soft drink, i.e. the opportunity cost of one bottle of wine is four bottles of soft drink.
AND Rice. 2.8.
 restrictions on income growth
restrictions on income growth
from the budget line equation
it follows that the budget line has a negative slope; the angle of its inclination is determined by the price ratio, and the distance from the origin of coordinates is determined by the size of the budget.
If, at fixed prices of goods, the consumer's budget changes, then a parallel shift in the budget line occurs.
The slope of the budget line will not change, since it is determined only by the price ratio. With an increase in income and constant prices, there will be a parallel upward shift in the budget line (Fig. 2.8). ER
This is explained by a change in the maximum quantity of consumption of the product
Zvenigorod College of Finance and Economics is a branch of the Financial University under the Government of the Russian Federation.
Report
in the discipline of economic theory on the topic of: "».
Budget lines
Completed by: student of group No. 26
Dergunova Ekaterina
Checked by: Orekhov N.A.
Zvenigorod, 2010
A budget line is a graphical way of describing a consumer's options.
Budget line
- the geometric locus of points of all possible combinations of goods X and Y, at which the total amount of costs for their acquisition is equal to the income that the consumer has to purchase these goods.
The budget line equation is:,
I = Px*Qx + Py*Qy
where I is disposable income;
Px, Py - prices of goods X and Y, respectively;
Qx, Qy - the quantity of goods X and Y, respectively.
Those. the consumer can purchase only those goods for which the costs are not
exceed the total amount of money at his disposal.
This equation shows the consumer's budget constraint. When depicting it graphically, we obtain the budget line.
The economic meaning of the intersection of the budget line with the coordinate axes is to express income in terms of the maximum quantity of a certain good that can be purchased with it.
A budget line is a graphical way of describing a consumer's options. The economic meaning of the slope of the budget line is that the additional quantity of good Y that a consumer can buy by sacrificing a unit of good X depends on the ratio of prices for these goods. Therefore, the tangent of the slope of the budget line is equal to the ratio of prices of goods, i.e. Rx/Ru.
- various combinations of two goods that can be
purchased at fixed amounts of cash income and certain prices. Budget lines answer the question: what can a consumer buy with a certain monetary income, taking into account current prices for goods.
Let us assume that good A costs 1.5 monetary units, and good B costs 1 monetary unit. A consumer with an income of 12 monetary units can purchase the following combinations of goods A and B:
Table 3 Combinations of goods A and B available to a buyer with an income of 12 monetary units.
Graph 6. Consumer budget line.
By combining the budget line and the indifference curve, we can answer the question of which combination of available goods will be most preferable.
This is usually the point where the highest indifference curve touches the budget line (y).

Graph 6. Combination of the budget line with the map of indifference curves.
Properties of the budget line:
1. The location of the budget line depends on the amount of monetary income. An increase in money income leads to a movement of the budget line to the right, a decrease - to the left.
2. Changes in product prices also lead to a shift in the budget line. A decrease in the prices of both products, equivalent to an increase in real income, moves the budget line to the right, an increase in product prices - to the left. When the price changes, the ratio P B / P A changes, therefore, the slope of the line changes.
A source of information:
http://works.tarefer.ru